Here at RADIO-TIMETRAVELLER I have two SDR radios in use. They are the SDRPlay RSPdx and the Airspy HF+ Discovery. The Airspy is by far the more sensitive and the one with the lowest noise floor. I use it both for mediumwave DXing and shortwave DXing. Antennas currently are a 44 ft. vee dipole on ground (a VDoG?) and a passive loop. The loop is the YouLoop, also by Airspy. It is a remarkable antenna when used with Airspy's HF+ Discovery on the medium waves.
 |
| Airspy HF+ Discovery |
Recently I've gotten into the also remarkable Co-Channel Canceller offered in the SDR# (SDR Sharp) software. This is becoming a very necessary tool to have in the DXing toolchest. It is particularly useful if using a wire antenna which is generally non-directional versus the YouLoop. Used with the YouLoop or other nulling loop, results can be even more dramatic.
The idea behind the Co-Channel Canceller is to minimize the effect of one station over another, the two (or more) carriers that might occupy the same channel. We are not just talking about "notching" a carrier here, but also notching or flooring a prescribed bandwidth around the chosen carrier as well.
 |
| The AM Co-Channel Canceler |
The key here is we need to know the exact frequency offset of that carrier down to the fraction of a Hertz (Hz) of all the carriers on the channel. There may be two, three, or many on channel.
The Micro Tuner
Enter the Micro Tuner, a neat and necessary little gadget also available as standard in SDR#. Bringing up the Micro Tuner plugin will show a spectrum display 10-30 Hertz wide surrounding the tuned frequency. It takes some time to settle in, but after a couple of minutes, each carrier peak surrounding the tuned frequency will be displayed. Here we are tuned to WHCU in Ithaca, New York on 870 KHz.
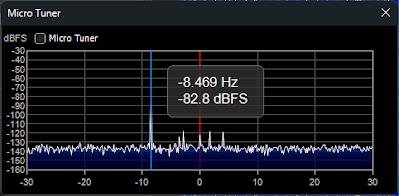 |
| The Micro Tuner |
WHCU, the strongest spike you see, is 8.469 Hz low in frequency, or a negative -8.469 offset. At least three other weaker carriers are present just above "0", as well as several noise spikes at about -3 Hz below 870 KHz.
Now, please understand that the Micro Tuner plugin is a separate plugin from the Co-Channel Canceller but can be used in different ways. In its elemental form, it can be enabled to allow micro-tuning of a signal, that is, positioning the tuned frequency on the exact carrier intended down to a fraction of a cycle. One must only enable it (just tick the checkbox), then click on a desired carrier peak in the graph. Try this sometime when in SSB mode (either USB or LSB).
In conjunction with the Co-Channel Canceller, we will use it to identify the exact carrier frequency offsets on the channel we are tuned to.
The Co-Channel Canceller
I'm using SDR# v.1920, the latest software version as of this writing. Others have said the Co-Channel Canceller works better using this latest version.
It is important to invoke the Micro Tuner and see exactly where the offensive station (and its carrier) is in relation to dead center "0", which is your tuned frequency. You need to set the Carrier Offset in the Co-Channel Canceller to this value.
To start, be sure you're using the DSB (double sideband) demodulation method. I recommend turning AGC ON. Set your receiver bandwidth to something comfortable but not too wide or too narrow, 4 to 6 KHz.
Tune to the frequency where you wish to engage the cancel feature. Example: I've been chasing a Cuban station on 670 KHz at sunrise lately. I typically have a rough time nulling WSCR 670 in Chicago, WSCR being the much stronger station. I tune to exactly 670.000 KHz.
Start the Micro Tuner and let it settle in. Drag the Micro Tuner's window width out fairly wide so you can see the detail better. Give it a couple of minutes to stabilize. DO NOT enable it. You probably will see several carriers. The strongest is likely the one you wish to remove. We just want to see the position of the carriers, not engage micro tuning.
Start up the Co-Channel Canceller (AM). Do the following in its settings:
1. Uncheck Remove Carrier.
2. Uncheck Auto Tune.
3. Allow bandwidth to settle at the same or as close to your chosen bandwidth (I use 5600 Hz for AM and DSB).
4. Set IF Offset to 0.000
5. Leave the Correction slider at midpoint.
Now for the important step.
6. Hover your mouse over the strongest carrier on the Micro Tuner. The tooltip will show the offset to "0", in Hertz, plus or minus. It may even be a fraction of one Hz, like 0.390.
Example: In the Cuban scenario described above, the WSCR carrier shows as +0.390 (from "0") on my Micro Tuner.
7. Set Carrier Offset on the Co-Channel Canceller to +0.390.
8. Engage (enable) the Co-Channel Canceller.
WSCR is gone.
While listening with the Co-Channel Canceller enabled, if you try scrolling the Carrier Offset setting through all values, minus through plus, you will find it best at the offset shown on the Micro Tuner.
Auto Tune attempts to guess at the right Carrier Offset, but results are less than desirable this way versus manually setting the offset to the exact value in the Micro Tuner.
I've had mixed results turning AGC off and controlling receiver gain with the attenuator. Even though I am in a high signal area I get better results with the canceller using AGC ON.
Experiment with the FFT filters. I have slightly better results with the basic "Sine" filter, not sure why.
Here's an example with an image, using the Micro Tuner to determine the offset, then plugging the offset into the Carrier Offset setting. We are tuned to 1120 KHz this time. My mouse is hovered over the big carrier to the left of "0", showing it's at -11.560 Hz. This is likely KMOX in St. Louis, Missouri. I then set the Carrier Offset to -11.560 and enable the Co-Channel Canceller.
 |
| Use of the Canceller and the Micro Tuner |
Notice that when you change the Carrier Offset in the box, the bandwidth may reduce, depending on the offset value. It will always be less than your receiver bandwidth setting. For the time being, let it settle where it will. My receiver bandwidth in this situation is 5600 Hz. Be sure you are in DSB demodulation mode. I've not had success in getting the Co-Channel Canceller to work in USB or LSB. AM is questionable too, though it may produce some odd results. Try RAW mode while you're at it. It does work fairly well but produces quite an echo, sort of a binaural stereo effect. To some ears this might be OK. It can enhance intelligibility some if you can tolerate the echo effect.
Some other notes gathered from further experimentation.
1. Checking Auto Tune seems to negate any value in the Carrier Offset box and the Canceller will attempt to find the "'right" carrier to cancel. Be sure Auto Tune is off. If you enable it, you will never know which carrier peak Auto Tune settles on. Generally, I suspect it is the strongest one, but many times the carriers are very close in strength.
2. Once set up as per the previous narrative, try checking Remove Carrier and you might find some interesting results, particularly if you have reduced the bandwidth setting in the Co-Channel Canceller plugin. The bandwidth setting seems to be the bandwidth "removed" surrounding the Carrier Offset setting. Try reducing the bandwidth to under 3000 Hz, and even down to within 500-1500 Hz. Good results can sometimes be had in that range, particularly when enabling Remove Carrier. Here it is important to remember we are removing "audio" bandwidth surrounding the offending carrier. Audio speech "punch", the range of best intelligibility, is between 300-3000 Hz. The Co-Channel Canceller bandwidth setting can work better within this range in certain situations.
3. IF Offset. At this point with some cancelling going, scroll the IF Offset to the right (plus) or left (minus) from the Carrier Offset, away from the cancelled carrier. This will move the passband above or below the cancelled carrier. I've had some very good results shifting the IF Offset 500-1000 Hz up or down.
4. Co-Channel Canceller has difficulty on channels having a lot of "side" splatter. Example: Received at night in the Rochester, NY area we have WGY 810, Schenectady severely splattered by CKLW 800, Windsor, Ontario. Trying the Co-Channel Canceller on 810 KHz had mixed results due to the 800 KHz splatter. Results will vary under these situations.
5. Finally, once you are satisfied with all your settings, play with the Correction slider. I've had some small, but positive results there. The Correction slider does not seem to be a "center" based control - plus or minus, but rather applies a linear amount of co-channel correction to the cancel operation. Setting it all the way to the right applies the maximum correction to the algorithm.
6. Think about this. Used with a rotatable loop antenna having good nulling properties, you have the option to remove two offending stations. First use the loop to null one station. Then, use the Co-Channel Canceller to remove a second station.
There you have it, a short course on how to use the SDR# Co-Channel Canceller.