1. Antenna efficiency. A mediumwave tower or array of towers will be more or less efficient depending on their radiation length(s). The FCC provides us with a figure called RMS Theoretical for every station's antenna array whether it be one tower or several, measured in mV/m. Reflected in this figure is the efficiency.
2. Pattern gain. Multiple tower arrays inherently have broadcast patterns. Meaning, of course, they aim to broadcast a majority of their signal in a certain direction to cover their market audience and/or avoid co-channel interference with another station. Where you are in relation to that pattern is important. If you are in the major lobe of a 50KW station, it may be pumping upwards of 100KW towards you, or more. If you are in a sharp pattern null, it may only be beaming hundreds of watts towards you. The amount of millivolts per meter "facing you" is the important figure. The FCC provides that as well, in their pattern plots.
There is only one case where we will need to do a simple extra calculation to arrive at the full millivolt per meter level for a station. That is for stations with a single tower only. I will explain why in just a minute.
So let's put together what we need. First, pick a station within reasonable distance you think you'd like to log. Note its frequency. Next, gather the following four things:
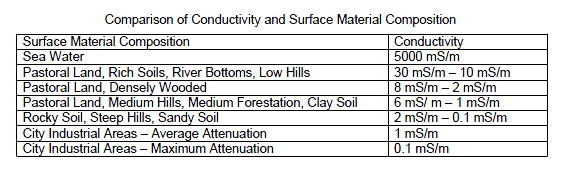
1. The ground conductivity in mS/m between you and the station. Use the M3 conductivity map. If the station path crosses a couple of zones, estimate the average ground conductivity for the entire path. The resultant figure should fall between 0.1 mS/m and 30 mS/m, or possibly higher if part of the path is over salt seawater.
2. The Ground Wave Field Strength Versus Distance graph for the frequency of the station, one of the 20 graphs published by the FCC. Several frequencies are usually grouped into one graph. The graphs are in .PDF form. Have your .PDF viewer ready.
3. You will need to find your distance to the station in kilometers, and also the reverse bearing from the station back to you. Many calculators exist on the web which will compute this information. The FCC has a good one, be sure to check out their calculator. These calculators require you to know the latitude and longitude of both your location and the station's location.
www.wikimapia.org is a great way to determine your home latitude and longitude as it has a crosshair defining the center of the map, and thus the latitude and longitude. Move the map to your exact location and read the latitude-longitude in the web browser's address bar.
The station's latitude and longitude can be found in a couple of ways. The FCC's AM Query web page allows us to query the station by call sign. The search output will display basic information like latitude and longitude. Click on the call sign link and you will be taken to the FCC's web page for the facility (station). Example: WHAM-1180 page.
4. The last item. Get the millivolt per meter value at 1 kilometer from the station transmitter, headed your way. The method of locating this figure will depend on whether the station has one antenna tower or multiple towers in its array.
Determine if the station uses a single tower or multiple towers for the service you are interested in. This information can be found on the FCC's web page for the facility (station), as shown just above.
Note that stations may have more than one entry on the page, one for each service they operate under, i.e., UNLIMITED, DAYTIME, NIGHTTIME, CRITICAL HOURS. Be sure you are looking at the correct service. Sometimes stations use a different number of towers for day and night.
mV/m for multiple towers.
The mV/m figure is gotten from the pattern data. It's simple.
Multiple tower arrays will give you the option to display the pattern plot. The pattern plot link will be under a heading that looks like this:
Horizontal Pattern at 1 km radius (Sections 73.150 and 73.152):
Electric Field Strength pattern plot
Pattern Data for WXXI
Either link will give us the information we need, though the "Electric Field Strength pattern plot" gives a nice graphic pattern plot for the station. Click one of the links.
RMS Theoretical values, and in some cases RMS Standard or even RMS Augmented values will be displayed for each five degrees of compass, 0-360. Find the compass bearing that most closely matches the return bearing from the station to you. We need to record one value only. Preferably, record the RMS Augmented value, if given. If not available, record the RMS Standard value. If not given, record the RMS Theoretical value. These values are in millivolts per meter and are the value of signal level the station presents towards you.
A quick definition of RMS Standard and RMS Augmented values. RMS Standard is essentially the RMS Theoretical value plus 5%. It is a "guard" against interference to other co-channel stations by overstating the RMS Theoretical calculated value. If stations have pattern augmentations, and many do, the RMS Augmented field will be present. Augmentations are enhancements or detractions to the theoretical pattern.
I'll use WXXI-1370 for the example. At night it runs 4 towers and has a roughly figure-8 pattern north-south. WXXI's return bearing to me is 204.7 degrees. Checking the FCC pattern plot for the station, we see that the 205 degree return azimuth presents a facing RMS Theoretical of 350.59 mV/m and a facing RMS Standard of 368.88 mV/m. We will use the RMS Standard value in the final calculation.
mV/m for single tower.
A special case requiring a simple calculation. We will calculate the mV/m figure from the RMS Theoretical value.
Again go to the FCC's web page for the facility (station), as above. The RMS Theoretical value will be on this page.
Note again that stations may have more than one entry on the page, one for each service they operate under, i.e., UNLIMITED, DAYTIME, NIGHTTIME, CRITICAL HOURS. Be sure you are looking at the correct service. Sometimes stations use a different number of towers for day and night.
The FCC computes all RMS Theoretical values from a formula of course. The values are calculated for a distance of 1 kilometer. The FCC formula used generates accurate millivolt per meter values (as published) for multiple tower arrays. Single tower arrays are a special case, however, in that the published mV/m value is always based on a 1 kilowatt output power calculation. Hence, the only published single tower mV/m values we can use are those of 1 KW stations. For all others, we will do a simple calculation to arrive at the correct mV/m value. Proof of this is simple. For example, check the FCC's published figures for my local WHAM-1180 station out of Rochester, NY. This 50KW station shows a calculated RMS Theoretical value at 1 kilometer of only 376.59 mV/m. Now of course this cannot be correct for a 50KW station, as a 1 KW station running a quarter wave (.250 wavelength) monopole has an exact calculated figure of 305.768 mV/m at 1 kilometer.
376.59 mV/m would, however, be correct for a 1 KW station using the same single tower antenna that WHAM uses (a .492 wavelength antenna).
To accurately calculate the mV/m figure for WHAM (or any other single tower station, including those 1 KW stations), the following formula must be applied:
(Power in KW, distance in KM):WHAM's actual RMS Theoretical value is 2662.89 mV/m. And since it is a single tower antenna having an omnidirectional pattern, it presents this value of signal in all directions. Use the value you calculate for your single tower station of interest as the mV/m value that the station presents towards you.
mV/m = RMSTheoretical x SQRoot(Power/Distance)
Thus in WHAM's case:
2662.89 = 376.59 * SQRoot(50/1)
Making The Calculation
Now we have all of our information. Let's get busy. We will use the FCC's Ground Wave Field Strength Versus Distance graph to arrive at the received mV/m signal level. Proceed with the following steps.
1. To make them universal, the FCC's Ground Wave Field Strength Versus Distance graphs are based on 100 mV/m levels at 1 kilometer. We simply need to calculate how many 100s our mV/m value is. Just move the decimal point left two places. In WHAM's case, 2662.89 mV/m, 26.6289 (26.6289 x 100 = 2662.89). The multiplier value we will use for WHAM is 26.6289. In WXXI's case, 368.88 mV/m, 3.6888 (3.6888 x 100 = 368.88). The multiplier value we will use for WXXI is 3.6888.
2. Find the station distance in kilometers on the graph, usually at the bottom. The bottom range is 10 to 1000 kilometers. The top range is 0.1 to 50 kilometers.
3. Draw a trace upwards (or downwards if using the top scale) until you hit the ground conductivity value curve that matches the average ground conductivity between you and the station.
4. From the previous point, draw a trace leftward to the scale on the left side of the graph. This is the base millivolt per meter level based on 100 mV/m at 1 kilometer. Multiply this value by your multiplier value. In WHAM's case, multiply times 26.6289. In WXXI's case, multiply times 3.6888. This resultant value is the received field strength in millivolts per meter at your location.
There you have it. You have ballparked the approximate field strength of your station of interest. If done correctly, you should find this in fairly good agreement with V-Soft's figure if you are near the zipcode point they based their calculation on. With a list of expected receive field strengths for various stations, you can judge the approximate sensitivity of your receiver. After a few times trying this, you will find the calculation to be rather simple to do.
Hope you have enjoyed this series.
If you are interested in the history of field strength calculations, be sure to see Field Strength Calculations: A History on RADIO-TIMETRAVELLER.